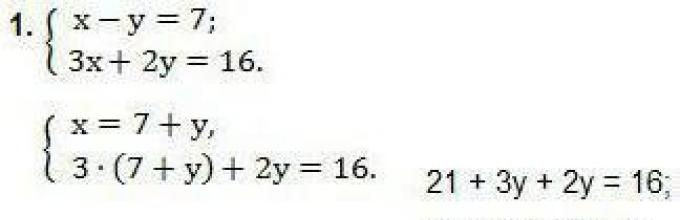Iqtisodiyot sohasida turli jarayonlarni matematik modellashtirish uchun tenglamalar tizimlari keng qo'llaniladi. Masalan, ishlab chiqarishni boshqarish va rejalashtirish, logistika yo'nalishlari (transport muammosi) yoki jihozlarni joylashtirish muammolarini hal qilishda.
Tenglamalar sistemasi nafaqat matematikada, balki fizika, kimyo va biologiyada ham aholi sonini topish masalalarini yechishda qo'llaniladi.
Tizim chiziqli tenglamalar umumiy yechim topish zarur bo'lgan bir nechta o'zgaruvchiga ega bo'lgan ikki yoki undan ortiq tenglamalarni nomlang. Barcha tenglamalar haqiqiy tenglikka aylanadigan yoki ketma-ketlik mavjud emasligini isbotlaydigan raqamlarning bunday ketma-ketligi.
Chiziqli tenglama
ax+by=c ko’rinishdagi tenglamalar chiziqli deyiladi. X, y belgilari - qiymati topilishi kerak bo'lgan noma'lumlar, b, a - o'zgaruvchilarning koeffitsientlari, c - tenglamaning erkin hadi.
Tenglamani chizib yechish to‘g‘ri chiziqqa o‘xshaydi, uning barcha nuqtalari ko‘phadning yechimlaridir.
Chiziqli tenglamalar sistemalarining turlari
Eng oddiy misollar ikkita o'zgaruvchisi X va Y bo'lgan chiziqli tenglamalar tizimi hisoblanadi.
F1(x, y) = 0 va F2(x, y) = 0, bu erda F1,2 funksiyalar va (x, y) funksiya o'zgaruvchilari.
Tenglamalar tizimini yechish - bu tizim haqiqiy tenglikka aylanadigan qiymatlarni (x, y) topish yoki x va y ning mos qiymatlari mavjud emasligini aniqlashni anglatadi.
Nuqtaning koordinatalari sifatida yozilgan juft qiymatlar (x, y) chiziqli tenglamalar tizimining yechimi deb ataladi.
Agar tizimlar bitta umumiy yechimga ega bo'lsa yoki hech qanday yechim mavjud bo'lmasa, ular ekvivalent deb ataladi.
Chiziqli tenglamalarning bir jinsli sistemalari - o'ng tomoni nolga teng bo'lgan tizimlar. Agar tenglik belgisidan keyingi o'ng qism qiymatga ega bo'lsa yoki funktsiya bilan ifodalangan bo'lsa, bunday tizim geterogendir.
O'zgaruvchilar soni ikkitadan ancha ko'p bo'lishi mumkin, keyin biz uchta yoki undan ko'p o'zgaruvchiga ega chiziqli tenglamalar tizimining misoli haqida gapirishimiz kerak.
Tizimlar bilan duch kelganda, maktab o'quvchilari tenglamalar soni noma'lumlar soniga to'g'ri kelishi kerak deb o'ylashadi, ammo bu unday emas. Tizimdagi tenglamalar soni o'zgaruvchilarga bog'liq emas, ular xohlagancha ko'p bo'lishi mumkin;
Tenglamalar sistemalarini yechishning oddiy va murakkab usullari
Bunday tizimlarni yechishning umumiy analitik usuli mavjud emas, barcha usullar sonli yechimlarga asoslangan; IN maktab kursi Matematika almashtirish, algebraik qo'shish, almashtirish, shuningdek, grafik va matritsa usullari, Gauss usuli bilan yechish kabi usullarni batafsil tavsiflaydi.
Yechish usullarini o'rgatishda asosiy vazifa tizimni to'g'ri tahlil qilishni va har bir misol uchun optimal yechim algoritmini topishni o'rgatishdir. Asosiysi, har bir usul uchun qoidalar va harakatlar tizimini yodlash emas, balki ma'lum bir usuldan foydalanish tamoyillarini tushunishdir.
7-sinf umumta’lim dasturida chiziqli tenglamalar sistemasiga misollar yechish juda oddiy va juda batafsil tushuntirilgan. Har qanday matematika darsligida ushbu bo'limga etarlicha e'tibor beriladi. Chiziqli tenglamalar sistemalariga misollarni Gauss va Kramer usuli yordamida yechish oliy ta’limning birinchi yillarida batafsil o‘rganiladi.
Tizimlarni almashtirish usuli yordamida yechish
O'zgartirish usulining harakatlari bir o'zgaruvchining qiymatini ikkinchisi bilan ifodalashga qaratilgan. Ifoda qolgan tenglamaga almashtiriladi, so'ngra u bitta o'zgaruvchili shaklga keltiriladi. Harakat tizimdagi noma'lumlar soniga qarab takrorlanadi
7-sinf chiziqli tenglamalar tizimi misoliga almashtirish usuli yordamida yechim keltiramiz:

Misoldan ko'rinib turibdiki, x o'zgaruvchisi F(X) = 7 + Y orqali ifodalangan. Natijada X o'rniga tizimning 2- tenglamasiga almashtirilgan ifoda 2-tenglamada bitta Y o'zgaruvchisini olishga yordam berdi. . Yechim bu misol qiyinchiliklarga olib kelmaydi va Y qiymatini olish imkonini beradi. Oxirgi qadam Bu qabul qilingan qiymatlarni tekshirish.
Chiziqli tenglamalar sistemasiga misolni almashtirish usuli bilan yechish har doim ham mumkin emas. Tenglamalar murakkab bo'lishi mumkin va o'zgaruvchini ikkinchi noma'lum bilan ifodalash keyingi hisob-kitoblar uchun juda og'ir bo'ladi. Tizimda 3 dan ortiq noma'lum bo'lsa, almashtirish yo'li bilan yechish ham o'rinsiz.
Chiziqli bir hil bo'lmagan tenglamalar sistemasiga misol yechimi:

Algebraik qo‘shish yordamida yechim
Qo'shish usulidan foydalangan holda tizimlar yechimlarini izlashda tenglamalar atama bo'yicha qo'shiladi va turli raqamlarga ko'paytiriladi. Matematik operatsiyalarning yakuniy maqsadi bitta o'zgaruvchidagi tenglamadir.

Ushbu usulni qo'llash amaliyot va kuzatishni talab qiladi. Chiziqli tenglamalar tizimini 3 yoki undan ortiq oʻzgaruvchi boʻlganda qoʻshish usuli yordamida yechish oson emas. Tenglamalar kasr va o'nli kasrlarni o'z ichiga olgan bo'lsa, algebraik qo'shish qulay.
Yechim algoritmi:
- Tenglamaning ikkala tomonini ma'lum songa ko'paytiring. Arifmetik operatsiya natijasida o'zgaruvchining koeffitsientlaridan biri 1 ga teng bo'lishi kerak.
- Hosil boʻlgan iborani termin boʻyicha qoʻshing va nomaʼlumlardan birini toping.
- Qolgan o'zgaruvchini topish uchun olingan qiymatni tizimning 2-tenglamasiga almashtiring.
Yangi o'zgaruvchini kiritish orqali hal qilish usuli
Agar tizim ikkitadan ko'p bo'lmagan tenglamalar uchun echim topishni talab qilsa, yangi o'zgaruvchi kiritilishi mumkin, shuningdek, noma'lumlar soni ikkitadan oshmasligi kerak;
Usul yangi o'zgaruvchini kiritish orqali tenglamalardan birini soddalashtirish uchun ishlatiladi. Yangi tenglama kiritilgan noma'lum uchun echiladi va olingan qiymatdan asl o'zgaruvchini aniqlash uchun foydalaniladi.

Misol shuni ko'rsatadiki, yangi t o'zgaruvchisini kiritish orqali tizimning 1-tenglamasini standart kvadrat uch a'zoga qisqartirish mumkin edi. Ko'phadni diskriminantni topib yechishingiz mumkin.
Diskriminantning qiymatini taniqli formuladan foydalanib topish kerak: D = b2 - 4*a*c, bu erda D - kerakli diskriminant, b, a, c - ko'phadning omillari. Berilgan misolda a=1, b=16, c=39, demak D=100. Agar diskriminant noldan katta bo'lsa, u holda ikkita yechim mavjud: t = -b±√D / 2*a, agar diskriminant noldan kichik bo'lsa, unda bitta yechim mavjud: x = -b / 2*a.
Olingan tizimlar uchun yechim qo'shish usuli bilan topiladi.
Tizimlarni echishning vizual usuli
3 ta tenglama tizimi uchun javob beradi. Usul tizimga kiritilgan har bir tenglamaning grafiklarini koordinata o'qi bo'yicha qurishdan iborat. Egri chiziqlarning kesishish nuqtalarining koordinatalari tizimning umumiy yechimi bo'ladi.
Grafik usul bir qator nuanslarga ega. Chiziqli tenglamalar sistemalarini vizual tarzda yechishning bir qancha misollarini ko‘rib chiqamiz.

Misoldan ko'rinib turibdiki, har bir chiziq uchun ikkita nuqta qurilgan, x o'zgaruvchisining qiymatlari o'zboshimchalik bilan tanlangan: 0 va 3. X qiymatlari asosida y uchun qiymatlar topildi: 3 va 0. Koordinatalari (0, 3) va (3, 0) bo'lgan nuqtalar grafikda belgilangan va chiziq bilan bog'langan.
Ikkinchi tenglama uchun qadamlar takrorlanishi kerak. Chiziqlarning kesishish nuqtasi tizimning yechimidir.
Quyidagi misol chiziqli tenglamalar sistemasining grafik yechimini topishni talab qiladi: 0,5x-y+2=0 va 0,5x-y-1=0.

Misoldan ko'rinib turibdiki, tizim hech qanday yechimga ega emas, chunki grafiklar parallel va butun uzunligi bo'ylab kesishmaydi.

2 va 3-misollardagi tizimlar bir-biriga o'xshash, ammo tuzilganida ularning echimlari boshqacha ekanligi ayon bo'ladi. Shuni esda tutish kerakki, tizimning yechimi bor yoki yo'qligini aytish har doim ham mumkin emas;
Matritsa va uning turlari
Matritsalar chiziqli tenglamalar tizimini ixcham yozish uchun ishlatiladi. Matritsa - bu raqamlar bilan to'ldirilgan maxsus jadval turi. n*m n - satr va m - ustunga ega.
Ustunlar va satrlar soni teng bo'lganda matritsa kvadrat hisoblanadi. Matritsa-vektor - cheksiz mumkin bo'lgan qatorlar soniga ega bo'lgan bitta ustunli matritsa. Diagonallardan biri va boshqa nol elementlari bo'ylab birlari bo'lgan matritsaga o'ziga xoslik deyiladi.
Teskari matritsa matritsa bo'lib, uni ko'paytirganda asl matritsa birlik matritsaga aylanadi;
Tenglamalar tizimini matritsaga aylantirish qoidalari
Tenglamalar sistemasiga nisbatan tenglamalarning koeffitsientlari va erkin shartlari matritsa sonlari sifatida yoziladi, bitta tenglama matritsaning bir qatoridir;
Agar satrning kamida bitta elementi nolga teng bo'lmasa, matritsa qatori nolga teng emas deyiladi. Shuning uchun, agar tenglamalarning birortasida o'zgaruvchilar soni farq qiladigan bo'lsa, unda etishmayotgan noma'lum o'rniga nol kiritish kerak.
Matritsa ustunlari o'zgaruvchilarga qat'iy mos kelishi kerak. Bu shuni anglatadiki, x o'zgaruvchining koeffitsientlari faqat bitta ustunda yozilishi mumkin, masalan, birinchi, noma'lum y koeffitsienti - faqat ikkinchisida.
Matritsani ko'paytirishda matritsaning barcha elementlari ketma-ket songa ko'paytiriladi.
Teskari matritsani topish variantlari
Teskari matritsani topish formulasi juda oddiy: K -1 = 1 / |K|, bu erda K -1 teskari matritsa va |K| matritsaning aniqlovchisi hisoblanadi. |K| nolga teng bo'lmasligi kerak, u holda tizim yechimga ega.
Determinant ikki-ikki matritsa uchun osongina hisoblab chiqiladi, siz faqat diagonal elementlarni bir-biriga ko'paytirishingiz kerak. “Uchdan uch” varianti uchun |K|=a 1 b 2 c 3 + a 1 b 3 c 2 + a 3 b 1 c 2 + a 2 b 3 c 1 + a 2 b 1 c 3 formulasi mavjud. + a 3 b 2 c 1. Siz formuladan foydalanishingiz mumkin yoki ishda ustunlar va elementlar qatorlari soni takrorlanmasligi uchun har bir satr va har bir ustundan bitta elementni olishingiz kerakligini eslashingiz mumkin.
Matritsa usuli yordamida chiziqli tenglamalar sistemasiga misollar yechish
Yechimni topishning matritsa usuli tizimlarni hal qilishda noqulay yozuvlarni kamaytirishga imkon beradi katta raqam o'zgaruvchilar va tenglamalar.

Misolda, a nm - tenglamalarning koeffitsientlari, matritsa - vektor x n - o'zgaruvchilar, b n - erkin shartlar.


Gauss usuli yordamida tizimlarni yechish
Oliy matematikada Gauss usuli Kramer usuli bilan birgalikda oʻrganiladi va tizimlar yechimlarini topish jarayoni Gauss-Kramer yechim usuli deb ataladi. Bu usullar ko'p sonli chiziqli tenglamalarga ega bo'lgan tizimlarning o'zgaruvchilarini topish uchun ishlatiladi.
Gauss usuli almashtirish va algebraik qoʻshish yoʻli bilan yechimlarga juda oʻxshaydi, lekin tizimliroqdir. Maktab kursida 3 va 4 tenglamalar sistemalari uchun Gauss usuli bilan yechim qo'llaniladi. Usulning maqsadi tizimni teskari trapezoid shakliga tushirishdir. Algebraik o'zgartirishlar va almashtirishlar yordamida bitta o'zgaruvchining qiymati tizim tenglamalaridan birida topiladi. Ikkinchi tenglama 2 ta noma'lumli ifoda, 3 va 4 esa mos ravishda 3 va 4 o'zgaruvchiga ega.
Tizimni tavsiflangan shaklga keltirgandan so'ng, keyingi yechim ma'lum o'zgaruvchilarni tizim tenglamalariga ketma-ket almashtirishga tushiriladi.
IN maktab darsliklari 7-sinf uchun Gauss usuli bo'yicha yechimning namunasi quyidagicha tasvirlangan:

Misoldan ko'rinib turibdiki, (3) bosqichda ikkita tenglama olingan: 3x 3 -2x 4 =11 va 3x 3 +2x 4 =7. Har qanday tenglamani echish sizga x n o'zgaruvchilardan birini topishga imkon beradi.

Matnda tilga olingan 5-teoremada aytilishicha, agar tizim tenglamalaridan biri ekvivalent bilan almashtirilsa, natijada hosil bo'lgan tizim ham asl tenglamaga teng bo'ladi.
Gauss usulini talabalar tushunishi qiyin o'rta maktab, lekin eng ko'plaridan biri qiziqarli usullar matematika va fizika darslarida chuqurlashtirilgan o‘quv dasturlariga kirgan bolalarning zukkoligini rivojlantirish.
Yozib olish qulayligi uchun hisob-kitoblar odatda quyidagicha amalga oshiriladi:

Tenglamalar va erkin atamalar koeffitsientlari matritsa shaklida yoziladi, bu erda matritsaning har bir qatori tizim tenglamalaridan biriga mos keladi. tenglamaning chap tomonini o'ngdan ajratadi. Rim raqamlari tizimdagi tenglamalar sonini bildiradi.
Birinchidan, ishlanadigan matritsani yozing, so'ngra qatorlardan biri bilan bajarilgan barcha harakatlar. Olingan matritsa "strelka" belgisidan keyin yoziladi va kerakli algebraik amallar natijaga erishilgunga qadar davom ettiriladi.
Natijada diagonallardan biri 1 ga teng, qolgan barcha koeffitsientlar esa nolga teng bo'lgan matritsa bo'lishi kerak, ya'ni matritsa birlik shakliga tushiriladi. Tenglamaning har ikki tomonida raqamlar bilan hisob-kitoblarni bajarishni unutmasligimiz kerak.
Ushbu yozib olish usuli unchalik mashaqqatli emas va ko'plab noma'lum narsalarni sanab, chalg'itmaslikka imkon beradi.
Har qanday yechim usulidan bepul foydalanish ehtiyotkorlik va biroz tajribani talab qiladi. Hamma usullar ham amaliy xususiyatga ega emas. Yechimlarni topishning ba'zi usullari inson faoliyatining muayyan sohasida afzalroq, boshqalari esa ta'lim maqsadlarida mavjud.
Tenglamalardan foydalanish hayotimizda keng tarqalgan. Ular ko'plab hisob-kitoblarda, inshootlarni qurishda va hatto sportda qo'llaniladi. Inson qadim zamonlarda tenglamalardan foydalangan va o'shandan beri ulardan foydalanish faqat ortib bordi. Shubhasiz, ko'p odamlar tenglama noma'lum bir xillik ekanligini bilishadi, bu tenglamani yechish va chap va o'ng tomonlarning teng qiymatlarini olish uchun aniqlanishi kerak. Ushbu turdagi tenglamani yechish uchun hamma narsani chapga siljitish kerak ma'lum qiymatlar, va o'ng tomonda hammasi noma'lum. Bu tenglamalarni 3 ta usul yordamida yechish mumkin:
1) almashtirishlar;
2) qo'shish;
3) fitna.
Usulni tanlash maqsadli tenglamaga bog'liq. Qaror qiling onlayn tenglama ikkita noma'lum bilan bu ko'plab saytlarda mumkin, ammo siz olingan natijaga ko'r-ko'rona ishonmasligingiz kerak.
Quyida 2 ta noma’lumli tenglamani qo‘shish usuli yordamida yechish misoli keltirilgan.
\[-9x + 5y = -40\]
Yechishni boshlash uchun birinchi narsa - har bir atamani ularning belgilarini hisobga olgan holda qo'shish:
\[-5y + 5y = 0\]
Ko'pgina hollarda, noma'lumni o'z ichiga olgan summalardan birida miqdor bo'ladi nolga teng. Tenglamani yechishning keyingi bosqichida olingan ma'lumotlardan tenglamani yaratishimiz kerak:
\[-7x + 0 = 21\]
Noma'lum narsani toping:
\[-7x = 21, x = 21 \div (-7) = -3\]
Olingan qiymatni har qanday asl tenglamaga kiriting va chiziqli tenglamani yechish orqali noma'lum 2 ni oling:
\[-6 - 5y = 61\]
\[-5y = 61 + 6\]
2 ta noma'lumli tenglamani onlayn qayerda yechish mumkin?
Siz https://site veb-saytidagi onlayn hal qiluvchi yordamida ikkita noma'lum tenglamani echishingiz mumkin.
Bepul onlayn hal qiluvchi har qanday murakkablikdagi onlayn tenglamalarni bir necha soniya ichida hal qilish imkonini beradi. Sizga kerak bo'lgan yagona narsa ma'lumotlaringizni hal qiluvchiga kiritishdir. Shuningdek, bizning veb-saytimizda video ko'rsatmalarni ko'rishingiz va tenglamani qanday echishni o'rganishingiz mumkin. Va agar sizda hali ham savollaringiz bo'lsa, ularni bizning VKontakte guruhimizda http://vk.com/pocketteacher so'rashingiz mumkin. Guruhimizga qo'shiling, biz har doim sizga yordam berishdan xursandmiz.Video darslik 2:
Tenglamalar sistemalarini yechish Ma'ruza:
Ikki noma'lumli eng oddiy tenglamalar tizimi
Ikki noma'lumli tenglamalar
Ushbu mavzuda ikkita noma'lumni o'z ichiga olgan tenglamalarni ko'rib chiqamiz. Ko'pincha, bu turdagi tenglamalarni echish uchun biz noma'lum bo'lgan tenglamalarga ega bo'lishimiz kerak.

Ikki noma'lumli tenglamalar quyidagi ko'rinishga ega: a, b, c, d - bu o'zgaruvchilarda bir-birining yonidagi raqamlar.
(x, y)- bu ikkala tenglamani to'g'ri tenglikka keltiradigan o'zgaruvchilar qiymatini topishni anglatadi.
Har bir tenglama bir nechta javobga ega bo'lishi mumkin, lekin tenglamalar tizimiga javob ikkala tenglamaga mos keladigan raqamlar juftligi bo'ladi.
Tenglamalar sistemasining yechimini analitik talqin qilish mumkin, ularning ba'zilarini keyinroq ko'rib chiqamiz va grafik.
Tenglamalar sistemasini yechishning grafik usuli
Berilgan tenglamalarning har biri uchun siz tekislikda o'zingizning grafigingizni qurishingiz mumkin - bu funktsiyaning ma'lum grafiklaridan biri bo'lishi mumkin. Grafiklar kesishgan nuqta tenglamalar tizimining yechimi bo'ladi. Bu nuqta o'z koordinatasiga ega bo'ladi, bu yechim bo'lgan ordinata va abscissaga mos keladi.
Grafikdan bir necha turdagi yechimlarni olish mumkin:
1. Ko'p echimlar. Masalan, bitta tenglama trigonometrik funktsiyani ifodalasa, ikkinchisi esa, masalan, OX o'qiga parallel bo'lgan to'g'ri chiziq bo'lsa, u holda bu to'g'ri chiziq ikkinchi funktsiya grafigini ma'lum bir davriylik bilan ko'p nuqtalarda kesib o'tadi.
2. Bitta yechim. Bunda funksiyalarning grafiklari bir nuqtada kesishadi. Odatda, bu rasm, agar tenglamalarning grafiklari to'g'ri chiziqlar bo'lsa, kuzatiladi.
3. Ikkita yechim. Ya'ni, tenglamalarning grafiklari ikkita nuqtada kesishadi. Bu odatda funksiyalardan birining grafigi parabola bo'lganda kuzatiladi.
4. Hech qanday yechim yo'q. Ayrim funksiya grafiklari umuman kesishmasligi mumkin, bu holda tizim yechimlarga ega bo‘lmaydi.
Analitik yechimning asosiy usullari
Grafik yordamida yechish har doim ham qulay emas, chunki funktsiyalarning kesishish nuqtasi koordinatalarning kelib chiqishidan ancha uzoqda bo'lishi mumkin yoki u kasr koordinatalariga ega bo'ladi. Tizimning yechimini eng aniq topish uchun analitik yechim usullaridan foydalanish yaxshiroqdir.
1. O'zgartirish
Tizimni almashtirish usuli yordamida yechish uchun tenglamalardan birida noma’lumlardan birini ifodalab, ikkinchi tenglamaga almashtirish kerak.

x = (c – tomonidan) / a
d (c – by) / a + ey = f
Ushbu almashtirishdan so'ng, tenglamalardan biri bitta noma'lum bo'ladi, shundan so'ng tenglama ma'lum usulda echiladi. O'zgaruvchilardan biri topilganda, uning qiymati birinchi tenglamaga almashtiriladi va shuning uchun ikkinchi o'zgaruvchi topiladi.
2. Tenglamalarni qo'shish yoki ayirish usuli
Bu usul noma'lumlardan biridan xalos bo'lishga imkon beradi. Shunday qilib, siz "x" o'zgaruvchisidan xalos bo'lishni xohlayotganingizni tasavvur qilaylik. Kimga bu usul sodir bo'lgan bo'lsa, birinchi tenglamani terminlar bo'yicha d ga, ikkinchi tenglamani esa a ga ko'paytirish kerak. Shundan so'ng siz "x" o'zgaruvchisi uchun bir xil koeffitsientlarni olasiz. Agar siz bir tenglamani boshqasidan ayirsangiz, bitta noma'lumdan xalos bo'lishingiz mumkin bo'ladi. Bundan tashqari, tenglama ma'lum usullar yordamida amalga oshiriladi.
| | |
Ikki noma'lumli chiziqli bo'lmagan tenglamalar
Ta'rif 1. A bir oz bo'lsin juft raqamlar to'plami (x; y). Aytishlaricha, A to'plami berilgan raqamli funktsiya z ikkita o'zgaruvchidan
x va y , agar A to'plamidagi har bir son juftligi ma'lum bir raqam bilan bog'langan qoida ko'rsatilgan bo'lsa. X va y ikkita o'zgaruvchining z raqamli funktsiyasini ko'rsatish ko'pincha bildirmoq
Shunday qilib: Qayerda (x , y) f
Qayerda (x , y) = – funksiyadan boshqa har qanday funksiya ,
ax+by+c
bu yerda a, b, c raqamlari berilgan. Ta'rif 3. Tenglamani yechish (2) x; y bir juft raqamlarga qo'ng'iroq qiling (
), buning uchun formula (2) haqiqiy tenglikdir.
1-misol. Tenglamani yeching

Har qanday sonning kvadrati manfiy bo'lmagani uchun (4) formuladan kelib chiqadiki, x va y noma'lumlar tenglamalar tizimini qanoatlantiradi.
yechimi sonlar juftligi (6; 3).
Javob: (6; 3)
2-misol. Tenglamani yeching Demak, (6) tenglamaning yechimi cheksiz son juft sonlar
(1 + y ; y) ,
mehribon
bu yerda y istalgan raqam.
chiziqli Ta'rif 4.

Tenglamalar sistemasini yechish x; y bir juft raqamlarga qo'ng'iroq qiling (
), ularni ushbu sistemaning har bir tenglamasiga almashtirganda, to'g'ri tenglik olinadi.

Ikki tenglamalar sistemalari, ulardan biri chiziqli, shaklga ega(x , y)
g
4-misol. Tenglamalar tizimini yechish


Yechim. (7) sistemaning birinchi tenglamasidan noma’lum y ni noma’lum x orqali ifodalaymiz va olingan ifodani sistemaning ikkinchi tenglamasiga almashtiramiz:
x 1 = - 1 , x 2 = 9 .
Tenglamani yechish
y 1 = 8 - x 1 = 9 ,
y 2 = 8 - x 2 = - 1 .


Demak,
Ikki tenglama sistemasi, ulardan biri bir jinsli

Bittasi bir jinsli bo'lgan ikkita tenglamalar tizimi shaklga ega Ikki tenglamalar sistemalari, ulardan biri chiziqli, shaklga ega(x , y) bu yerda a, b, c raqamlari berilgan va
– ikkita o‘zgaruvchining x va y funksiyasi.
6-misol. Tenglamalar tizimini yechish
3x 2 + 2Yechim. Keling, bir jinsli tenglamani yechamiz - y 2 = 0 ,
3x 2 + 17Yechim. Keling, bir jinsli tenglamani yechamiz + 10y 2 = 0 ,
xy
 .
.
noma'lum x ga nisbatan kvadrat tenglama sifatida qaralsa: x = - 5y Bo'lgan holatda
5y 2 = - 20 ,
, (11) sistemaning ikkinchi tenglamasidan tenglamani olamiz
ildizi yo'q.
Bo'lgan holatda
 ,
,
(11) sistemaning ikkinchi tenglamasidan tenglamani olamiz y 1 = 3 , y 2 = - 3 . ularning ildizlari raqamlardir
Ushbu qiymatlarning har biri uchun mos keladigan x qiymatini topib, tizimning ikkita yechimini olamiz: (- 2 ; 3) , (2 ; - 3) .
Javob: (- 2 ; 3) , (2 ; - 3)
Boshqa turdagi tenglamalar tizimini yechishga misollar
Yechim. Formulalar bo'yicha x va y orqali ifodalangan yangi u va v noma'lumlarni kiritamiz:
(12) sistemani yangi noma’lumlar ko‘rinishida qayta yozish uchun avvalo x va y noma’lumlarni u va v orqali ifodalaymiz. (13) tizimdan shunday xulosa kelib chiqadi
Chiziqli sistemani (14) bu sistemaning ikkinchi tenglamasidan x o'zgaruvchini chiqarib echamiz.
- Buning uchun (14) tizimda quyidagi o'zgarishlarni amalga oshiramiz:
- Biz tizimning birinchi tenglamasini o'zgarishsiz qoldiramiz;
ikkinchi tenglamadan birinchi tenglamani ayiramiz va sistemaning ikkinchi tenglamasini hosil bo'lgan farq bilan almashtiramiz.

Natijada (14) sistema ekvivalent sistemaga aylanadi
undan topamiz
Formulalar (13) va (15) yordamida biz dastlabki tizimni (12) shaklda qayta yozamiz
(16) sistemaning birinchi tenglamasi chiziqli, shuning uchun undan noma’lum u ni noma’lum v orqali ifodalashimiz va bu ifodani sistemaning ikkinchi tenglamasiga almashtirishimiz mumkin.
8-bob. Tenglamalar sistemalari
8.2. Ikki noma'lumli ikkita chiziqli tenglamalar tizimi
Ta'rif Xuddi shu noma'lumlar bir xil miqdorni bildiradigan bir nechta tenglamalar deyiladi.
tenglamalar tizimi Tur tizimi deyiladi normal shakl
ikkita noma'lumli ikkita chiziqli tenglamalar tizimi.
Bunday sistemani yechish har ikkala tenglama uchun umumiy barcha yechimlar to'plamini topishni anglatadi.
Bunday tizimni qanday hal qilish mumkin?
Bunday tizimni, masalan, grafik tarzda hal qilish mumkin. Odatda, bunday tizim grafik jihatdan ikkita to'g'ri chiziq bilan ifodalanadi va bu tenglamalarning umumiy yechimi (tizimning yechimi) ikkita to'g'ri chiziqning umumiy nuqtasining koordinatalari bo'ladi. Bu erda uchta mumkin bo'lgan holatlar mavjud:
1) To'g'ri chiziqlar (grafiklar) faqat bitta umumiy nuqtaga ega (kesishadi) - tenglamalar tizimi yagona yechimga ega va u aniq deyiladi. 2) To'g'ridan-to'g'ri (grafiklar) mavjud emas umumiy nuqtalar
(parallel) - tizim yechimga ega emas va nomuvofiq deb ataladi.
3) To'g'ri chiziqlar (grafiklar) cheksiz ko'p umumiy nuqtalarga ega (mos keladi) - tizim cheksiz miqdordagi echimlarga ega va noaniq deb ataladi.
Men hali tushunmagan narsam bor. Balki misollar bilan aniqroq bo'lar?
Albatta, endi biz har bir holat uchun misol keltiramiz va hamma narsa darhol aniq bo'ladi.
Tizim aniqlanganda (yagona yechimga ega) misol bilan boshlaylik. Keling, tizimni olaylik. Keling, ushbu funksiyalarning grafiklarini tuzamiz.
Ular faqat bir nuqtada kesishadi, shuning uchun bu sistemaning yechimi faqat nuqtaning koordinatalari hisoblanadi: , .
Bunday holda, tizim qarama-qarshidir: chap qismlar teng, lekin o'ng qismlar boshqacha. Grafiklarda umumiy nuqtalar (parallel) yo'q, shuning uchun tizimda yechim yo'q.
Xo'sh, endi tizim noaniq bo'lgan oxirgi holat mavjud (cheksiz miqdordagi echimlarga ega). Mana shunday tizimga misol: . Keling, ushbu tenglamalarni tuzamiz.
To'g'ri chiziqlar (grafiklar) cheksiz ko'p umumiy nuqtalarga ega (mos keladi), ya'ni tizim cheksiz miqdordagi echimlarga ega. Bunday holda, tizim tenglamalari ekvivalent bo'ladi (ikkinchi tenglamani ko'paytirish 2 , biz birinchi tenglamani olamiz).
Eng muhimi, birinchi holat. Bunday tizimning yagona yechimini har doim grafik tarzda topish mumkin - ba'zan aniq va ko'pincha taxminan kerakli darajada aniqlik bilan.
8.2. Ikki noma'lumli ikkita chiziqli tenglamalar tizimi
Ikki tenglamalar tizimi ekvivalent deyiladi (ekvivalent), agar ularning har birining barcha yechimlari ham ikkinchisining yechimi bo'lsa (yechimlar to'plami mos kelsa) yoki ikkalasining yechimi bo'lmasa.