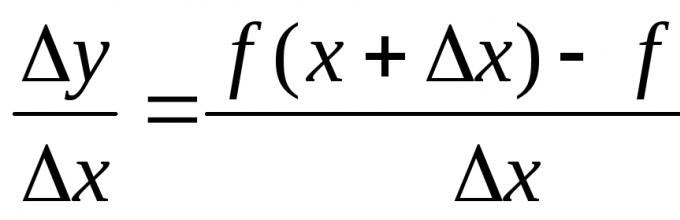Qaror qabul qilganda turli vazifalar geometriya, mexanika, fizika va boshqa bilim sohalari ushbu funktsiyadan bir xil analitik jarayon yordamida zarur bo'ldi. y=f(x) deb nomlangan yangi funktsiyani oling hosila funksiyasi(yoki shunchaki berilgan f(x) funksiyaning hosilasi va belgisi bilan belgilanadi
Berilgan funksiyadan kelib chiqadigan jarayon f(x) yangi xususiyatga ega bo'ling f" (x), chaqirildi farqlash va u quyidagi uch bosqichdan iborat: 1) dalil keltiring x oshirish
x va funktsiyaning mos keladigan o'sishini aniqlang
y = f(x+
x) -f(x); 
2) munosabat hosil qiling x 3) hisoblash
x doimiy va  0, topamiz f" (x), biz bilan belgilaymiz x, go'yo natijaviy funktsiya faqat qiymatga bog'liqligini ta'kidlaydi , bunda biz chegaraga boramiz.:
Ta'rif
y " =f " (x) hosilasi
y=f(x) funksiya berilgan berilgan x uchun
0, topamiz f" (x), biz bilan belgilaymiz x, go'yo natijaviy funktsiya faqat qiymatga bog'liqligini ta'kidlaydi , bunda biz chegaraga boramiz.:
Ta'rif
y " =f " (x) hosilasi
y=f(x) funksiya berilgan berilgan x uchun  funktsiya o'sishining argument o'sishiga nisbati chegarasi deyiladi, agar argumentning o'sishi nolga moyil bo'lsa, agar, albatta, bu chegara mavjud bo'lsa, ya'ni. cheklangan.
funktsiya o'sishining argument o'sishiga nisbati chegarasi deyiladi, agar argumentning o'sishi nolga moyil bo'lsa, agar, albatta, bu chegara mavjud bo'lsa, ya'ni. cheklangan. 
Shunday qilib, x, yoki E'tibor bering, agar biron bir qiymat uchun, masalan, qachon  x=a
x, munosabat f(x) da E'tibor bering, agar biron bir qiymat uchun0 chekli chegaraga moyil emas, u holda bu holda ular funktsiyani aytadilar E'tibor bering, agar biron bir qiymat uchun da E'tibor bering, agar biron bir qiymat uchun.
x=a
x, munosabat f(x) da E'tibor bering, agar biron bir qiymat uchun0 chekli chegaraga moyil emas, u holda bu holda ular funktsiyani aytadilar E'tibor bering, agar biron bir qiymat uchun da E'tibor bering, agar biron bir qiymat uchun.
(yoki nuqtada
) hosilasi yo‘q yoki nuqtada differensiallanmaydi

f(x)
2. Hosilning geometrik ma’nosi.
x 0 nuqtaga yaqin joyda differensiallanuvchi y = f (x) funksiya grafigini ko‘rib chiqaylik.
Funksiya grafigidagi nuqta - A(x 0, f (x 0)) nuqtadan o‘tuvchi va grafani qandaydir B(x;f(x)) nuqtada kesib o‘tuvchi ixtiyoriy to‘g‘ri chiziqni ko‘rib chiqaylik. Bunday chiziq (AB) sekant deb ataladi. ∆ABC dan: AC = ∆x;
BC =∆u; tgb=∆y/∆x.  AC ||dan beri Ox, keyin ALO = BAC = b (parallel uchun mos ravishda). Lekin ALO - AB sekantining Ox o'qining musbat yo'nalishiga moyillik burchagi. Bu tanb = k AB to'g'ri chiziqning burchak koeffitsienti ekanligini anglatadi.
AC ||dan beri Ox, keyin ALO = BAC = b (parallel uchun mos ravishda). Lekin ALO - AB sekantining Ox o'qining musbat yo'nalishiga moyillik burchagi. Bu tanb = k AB to'g'ri chiziqning burchak koeffitsienti ekanligini anglatadi.  Endi biz ∆x ni kamaytiramiz, ya'ni. ∆x→ 0. Bunda B nuqta grafik bo‘yicha A nuqtaga yaqinlashadi va AB sekant aylana oladi. AB sekantining ∆x→ 0 nuqtadagi chegaralovchi pozitsiyasi A nuqtadagi y = f (x) funktsiya grafigiga teginish deb ataladigan to'g'ri chiziq (a) bo'ladi.
Endi biz ∆x ni kamaytiramiz, ya'ni. ∆x→ 0. Bunda B nuqta grafik bo‘yicha A nuqtaga yaqinlashadi va AB sekant aylana oladi. AB sekantining ∆x→ 0 nuqtadagi chegaralovchi pozitsiyasi A nuqtadagi y = f (x) funktsiya grafigiga teginish deb ataladigan to'g'ri chiziq (a) bo'ladi.  Agar tgb =∆y/∆x tengligida ∆x → 0 sifatida chegaraga chiqsak, hosil bo‘ladi.
Agar tgb =∆y/∆x tengligida ∆x → 0 sifatida chegaraga chiqsak, hosil bo‘ladi.
ortg =f "(x 0), chunki
Funksiyaning x nuqtadagi hosilasi 0 abscissa x nuqtada chizilgan funksiya grafigiga teginish qiyaligiga teng. 0 .
3. Hosilning fizik ma’nosi.
Nuqtaning to‘g‘ri chiziq bo‘ylab harakatini ko‘rib chiqaylik. Nuqtaning istalgan vaqtda x(t) koordinatasi berilsin. Ma'lumki (fizika kursidan) ma'lum vaqt oralig'idagi o'rtacha tezlik bu vaqt davomida bosib o'tgan masofaning vaqtga nisbatiga teng, ya'ni.
Vav = ∆x/∆t. Oxirgi tenglikdagi chegaraga ∆t → 0 sifatida o‘tamiz.
lim Vav (t) = (t 0) - t 0, ∆t → 0 vaqtidagi oniy tezlik.
va lim = ∆x/∆t = x"(t 0) (hosilning ta'rifi bo'yicha).
Demak, (t) =x"(t).
Hosilning fizik ma'nosi quyidagicha: funktsiyaning hosilasiy = f(x) nuqtadax 0 funktsiyaning o'zgarish tezligif(x) nuqtadax 0
Bu hosila fizikada koordinatalarning vaqtga nisbatan maʼlum funksiyasidan tezlikni, tezlikning vaqtga nisbatan maʼlum funksiyasidan tezlanishni topish uchun ishlatiladi.
(t) = x"(t) - tezlik,
a(f) = "(t) - tezlanish, yoki
Agar aylanadagi moddiy nuqtaning harakat qonuni ma'lum bo'lsa, u holda aylanish harakati paytida burchak tezligi va burchak tezlanishini topish mumkin:
ph = ph(t) - burchakning vaqt o'tishi bilan o'zgarishi,
ō = ph"(t) - burchak tezligi,
e = ph"(t) - burchak tezlanishi yoki e = ph"(t).
Agar bir jinsli bo'lmagan tayoqning massa taqsimot qonuni ma'lum bo'lsa, unda bir jinsli bo'lmagan tayoqning chiziqli zichligini topish mumkin:
m = m(x) - massa,
x , l - novda uzunligi,
p = m"(x) - chiziqli zichlik.
Hosildan foydalanib, elastiklik va garmonik tebranishlar nazariyasiga oid masalalar yechiladi. Shunday qilib, Guk qonuniga ko'ra
F = -kx, x - o'zgaruvchan koordinata, k - bahor elastiklik koeffitsienti. ō 2 =k/m ni qo‘yib, prujinali mayatnikning x"(t) + ō 2 x(t) = 0 differensial tenglamasini olamiz,
bu erda ō = √k/√m tebranish chastotasi (l/c), k - kamon qattiqligi (H/m).
y" + ō 2 y = 0 ko'rinishdagi tenglama garmonik tebranishlar tenglamasi (mexanik, elektr, elektromagnit) deyiladi. Bunday tenglamalarning yechimi funktsiyadir.
y = Asin(ōt + ph 0) yoki y = Acos(ōt + ph 0), bu erda
A - tebranishlar amplitudasi, ō - siklik chastotasi,
ph 0 - dastlabki bosqich.
B9 muammosi funksiya yoki hosila grafigini beradi, undan quyidagi miqdorlardan birini aniqlash kerak:
- X 0 nuqtadagi hosilaning qiymati,
- Maksimal yoki minimal ball (ekstremum ball),
- Ortib boruvchi va kamayuvchi funksiyalar intervallari (monotonlik oraliqlari).
Bu masalada keltirilgan funksiyalar va hosilalar doimo uzluksiz bo‘lib, yechimni ancha osonlashtiradi. Topshiriq matematik tahlil bo'limiga tegishli bo'lishiga qaramay, hatto eng zaif talabalar ham buni qila oladilar, chunki bu erda chuqur nazariy bilim talab qilinmaydi.
Losmalar, ekstremum nuqtalar va monotonlik oraliqlarining qiymatini topish uchun oddiy va universal algoritmlar mavjud - ularning barchasi quyida muhokama qilinadi.
Ahmoqona xatolarga yo'l qo'ymaslik uchun B9 muammosining shartlarini diqqat bilan o'qing: ba'zida siz juda uzun matnlarga duch kelasiz, lekin muhim shartlar, qaror qabul qilish jarayoniga ta'sir qiladigan, bir nechtasi bor.
Hosila qiymatini hisoblash. Ikki nuqta usuli
Agar muammoga f(x) funksiyaning grafigi qaysidir x 0 nuqtasida shu grafaga tangens berilgan bo‘lsa va bu nuqtada hosilaning qiymatini topish talab etilsa, quyidagi algoritm qo‘llaniladi:
- Tangens grafigida ikkita "adekvat" nuqtani toping: ularning koordinatalari butun son bo'lishi kerak. Bu nuqtalarni A (x 1 ; y 1) va B (x 2 ; y 2) deb belgilaymiz. Koordinatalarni to'g'ri yozing - bu yechimning asosiy nuqtasi va bu erda har qanday xato noto'g'ri javobga olib keladi.
- Koordinatalarni bilgan holda, Dx = x 2 − x 1 argumentining ortishi va Dy = y 2 − y 1 funksiyasining o‘sishini hisoblash oson.
- Nihoyat, hosila D = Dy/Dx qiymatini topamiz. Boshqacha qilib aytganda, funktsiyaning o'sishini argumentning o'sishiga bo'lish kerak - va bu javob bo'ladi.
Yana bir bor eslatib o'tamiz: A va B nuqtalarni ko'pincha sodir bo'lganidek f(x) funksiya grafigidan emas, balki aniq tangensdan izlash kerak. Tangens chizig'ida kamida ikkita bunday nuqta bo'lishi kerak - aks holda muammo to'g'ri tuzilmaydi.
A (−3; 2) va B (−1; 6) nuqtalarini ko‘rib chiqing va o‘sishlarni toping:
Dx = x 2 - x 1 = -1 - (-3) = 2; Dy = y 2 - y 1 = 6 - 2 = 4.
Hosilaning qiymati topilsin: D = Dy/Dx = 4/2 = 2.
Vazifa. Rasmda y = f(x) funksiyaning grafigi va abtsissa x 0 nuqtada unga teginish ko'rsatilgan. f(x) funksiyaning x 0 nuqtadagi hosilasi qiymatini toping.
A (0; 3) va B (3; 0) nuqtalarini ko'rib chiqing, o'sishlarni toping:
Dx = x 2 - x 1 = 3 - 0 = 3; Dy = y 2 - y 1 = 0 - 3 = -3.
Endi hosila qiymatini topamiz: D = Dy/Dx = -3/3 = -1.
Vazifa. Rasmda y = f(x) funksiyaning grafigi va abtsissa x 0 nuqtada unga teginish ko'rsatilgan. f(x) funksiyaning x 0 nuqtadagi hosilasi qiymatini toping.
A (0; 2) va B (5; 2) nuqtalarini ko'rib chiqing va o'sishlarni toping:
Dx = x 2 - x 1 = 5 - 0 = 5; Dy = y 2 - y 1 = 2 - 2 = 0.
Hosilaning qiymatini topish qoladi: D = Dy/Dx = 0/5 = 0.
Oxirgi misoldan biz qoidani shakllantirishimiz mumkin: agar tangens OX o'qiga parallel bo'lsa, teginish nuqtasida funktsiyaning hosilasi nolga teng. Bunday holda, siz hech narsani hisoblashingiz shart emas - shunchaki grafikaga qarang.
Maksimal va minimal ballarni hisoblash
Ba'zan B9 masalada funktsiya grafigi o'rniga hosila grafigi beriladi va funktsiyaning maksimal yoki minimal nuqtasini topish talab etiladi. Bunday vaziyatda ikki nuqtali usul foydasiz, ammo boshqa, undan ham oddiyroq algoritm mavjud. Birinchidan, terminologiyani aniqlaymiz:
- x 0 nuqtasi f(x) funksiyaning maksimal nuqtasi deyiladi, agar bu nuqtaning qaysidir qo'shnisida quyidagi tengsizlik bajarilsa: f(x 0) ≥ f(x).
- x 0 nuqtasi f(x) funksiyaning minimal nuqtasi deyiladi, agar shu nuqtaning qaysidir qo'shnisida quyidagi tengsizlik bajarilsa: f(x 0) ≤ f(x).
Hosil grafigidan maksimal va minimal nuqtalarni topish uchun quyidagi amallarni bajaring:
- Barcha keraksiz ma'lumotlarni olib tashlagan holda lotin grafigini qayta chizing. Amaliyot shuni ko'rsatadiki, keraksiz ma'lumotlar faqat qaror qabul qilishga xalaqit beradi. Shuning uchun biz koordinata o'qida lotinning nollarini belgilaymiz - va bu.
- Nollar orasidagi intervallardagi hosila belgilarini toping. Agar biron bir x 0 nuqtasi uchun f'(x 0) ≠ 0 ekanligi ma'lum bo'lsa, u holda faqat ikkita variant mumkin: f'(x 0) ≥ 0 yoki f'(x 0) ≤ 0. Hosilning belgisi: dastlabki chizmadan aniqlash oson: agar hosilaviy grafik OX oʻqidan yuqorida joylashgan boʻlsa, f'(x) ≥ 0. Va aksincha, hosila grafik OX oʻqi ostida yotsa, f'(x) ≤ 0 boʻladi.
- Biz lotinning nollarini va belgilarini yana tekshiramiz. Belgining minusdan plyusga o'zgarishi minimal nuqtadir. Aksincha, lotin belgisi ortiqcha dan minusga o'zgartirilsa, bu maksimal nuqtadir. Hisoblash har doim chapdan o'ngga amalga oshiriladi.
Ushbu sxema faqat uzluksiz funktsiyalar uchun ishlaydi - B9 muammosida boshqa yo'q.
Vazifa. Rasmda f(x) funksiyaning [−5 oraliqda aniqlangan hosilasining grafigi ko'rsatilgan; 5]. f(x) funksiyaning shu segmentdagi minimal nuqtasini toping.
Keling, keraksiz ma'lumotlardan xalos bo'laylik va faqat chegaralarni qoldiramiz [−5; 5] va hosila nollari x = -3 va x = 2,5. Shuningdek, biz belgilarga e'tibor qaratamiz:
Shubhasiz, x = −3 nuqtada hosilaning belgisi minusdan plyusga o'zgaradi. Bu minimal nuqta.
Vazifa. Rasmda f(x) funksiyaning [−3 oraliqda aniqlangan hosilasining grafigi ko'rsatilgan; 7]. f(x) funksiyaning shu segmentdagi maksimal nuqtasini toping.
Keling, faqat chegaralarni qoldirib, grafikni qayta chizamiz [−3; 7] va hosila nollari x = −1,7 va x = 5. Hosil bo‘lgan grafikdagi hosilaning belgilarini qayd qilaylik. Bizda ... bor:
![]()
Shubhasiz, x = 5 nuqtasida lotin belgisi ortiqcha dan minusga o'zgaradi - bu maksimal nuqta.
Vazifa. Rasmda f(x) funksiyaning [−6 oraliqda aniqlangan hosilasining grafigi ko'rsatilgan; 4]. f(x) funksiyaning [−4” segmentiga tegishli maksimal nuqtalari sonini toping; 3].
Masalaning shartlaridan kelib chiqadiki, grafikning faqat segment bilan chegaralangan qismini ko'rib chiqish kifoya [−4; 3]. Shuning uchun biz quryapmiz yangi jadval, unda biz faqat chegaralarni belgilaymiz [-4; 3] va uning ichidagi hosilaning nollari. Ya'ni, x = -3,5 va x = 2 nuqtalari. Biz quyidagilarni olamiz:
![]()
Bu grafikda faqat bitta maksimal nuqta x = 2. Aynan shu nuqtada hosilaning belgisi ortiqcha dan minusga o'zgaradi.
Butun son bo'lmagan koordinatali nuqtalar haqida kichik eslatma. Masalan, oxirgi masalada x = -3,5 nuqtasi ko'rib chiqildi, ammo xuddi shu muvaffaqiyat bilan biz x = -3,4 ni olishimiz mumkin. Agar muammo to'g'ri tuzilgan bo'lsa, bunday o'zgarishlar javobga ta'sir qilmasligi kerak, chunki "belgilangan yashash joyisiz" nuqtalar muammoni hal qilishda bevosita ishtirok etmaydi. Albatta, bu hiyla butun sonlar bilan ishlamaydi.
O'sish va kamayuvchi funktsiyalarning intervallarini topish
Bunday masalada maksimal va minimal nuqtalar kabi, funktsiyaning o'zi ortib yoki kamayadigan sohalarni topish uchun hosilaviy grafikdan foydalanish taklif etiladi. Birinchidan, o'sish va kamayish nima ekanligini aniqlaymiz:
- Agar ushbu segmentning istalgan ikkita x 1 va x 2 nuqtalari uchun quyidagi fikr to'g'ri bo'lsa, f(x) funksiya segmentda ortib borayotgan deyiladi: x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2) . Boshqacha qilib aytganda, argument qiymati qanchalik katta bo'lsa, funktsiya qiymati shunchalik katta bo'ladi.
- f(x) funksiya, agar bu segmentning istalgan ikkita x 1 va x 2 nuqtalari uchun quyidagi fikr to'g'ri bo'lsa, segmentdagi kamayuvchi deyiladi: x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2). Bular. Kattaroq argument qiymati kichikroq funktsiya qiymatiga mos keladi.
Keling, oshirish va kamaytirish uchun etarli shartlarni tuzamiz:
- Uzluksiz f(x) funksiyaning segmentda ortishi uchun uning segment ichidagi hosilasi musbat bo'lishi kifoya, ya'ni. f’(x) ≥ 0.
- Uzluksiz f(x) funksiya segmentida kamayishi uchun uning segment ichidagi hosilasi manfiy bo'lishi kifoya, ya'ni. f’(x) ≤ 0.
Keling, bu gaplarni dalilsiz qabul qilaylik. Shunday qilib, biz o'sish va pasayish oraliqlarini topish sxemasini olamiz, bu ko'p jihatdan ekstremum nuqtalarni hisoblash algoritmiga o'xshaydi:
- Barcha keraksiz ma'lumotlarni olib tashlang. Hosilning asl grafigida bizni birinchi navbatda funksiyaning nollari qiziqtiradi, shuning uchun biz faqat ularni qoldiramiz.
- Nol orasidagi oraliqda hosilaning belgilarini belgilang. f’(x) ≥ 0 bo’lgan joyda funksiya ortadi, f’(x) ≤ 0 bo’lsa, u kamayadi. Agar muammo x o'zgaruvchisiga cheklovlar qo'ygan bo'lsa, biz ularni qo'shimcha ravishda yangi grafikda belgilaymiz.
- Endi biz funktsiyaning xatti-harakati va cheklovlarni bilganimizdan so'ng, muammoda talab qilinadigan miqdorni hisoblash qoladi.
Vazifa. Rasmda f(x) funksiyaning [−3 oraliqda aniqlangan hosilasining grafigi ko'rsatilgan; 7.5]. f(x) funksiyaning kamayish oraliqlarini toping. Javobingizda ushbu intervallarga kiritilgan butun sonlar yig'indisini ko'rsating.
Odatdagidek, grafikni qayta chizamiz va chegaralarni belgilaymiz [−3; 7.5], shuningdek x = -1.5 va x = 5.3 hosilasining nollari. Keyin hosila belgilarini qayd etamiz. Bizda ... bor:
![]()
(− 1,5) oraliqda hosila manfiy bo‘lgani uchun bu funksiya kamayuvchi intervaldir. Bu oraliq ichidagi barcha butun sonlarni yig'ish uchun qoladi:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.
Vazifa. Rasmda f(x) funksiyaning [−10 oraliqda aniqlangan hosilasining grafigi ko'rsatilgan; 4]. f(x) funksiyaning ortish oraliqlarini toping. Javobingizda ulardan eng kattasining uzunligini ko'rsating.
Keling, keraksiz ma'lumotlardan xalos bo'laylik. Keling, faqat chegaralarni qoldiramiz [−10; 4] va hosilaning nollari, bu safar ulardan to‘rttasi bor edi: x = −8, x = −6, x = −3 va x = 2. Hosilning belgilarini belgilaymiz va quyidagi rasmni olamiz:
Biz funktsiyani oshirish intervallari bilan qiziqamiz, ya'ni. f’(x) ≥ 0. Grafikda ikkita shunday interval mavjud: (−8; −6) va (−3; 2). Keling, ularning uzunligini hisoblaylik:
l 1 = - 6 - (-8) = 2;
l 2 = 2 - (−3) = 5.
Intervallarning eng kattasining uzunligini topishimiz kerakligi sababli, javob sifatida l 2 = 5 qiymatini yozamiz.
Funktsiyaning hosilasi eng qiyin mavzulardan biridir maktab o'quv dasturi. Har bir bitiruvchi lotin nima degan savolga javob bermaydi.
Ushbu maqola lotin nima ekanligini va nima uchun kerakligini sodda va tushunarli tarzda tushuntiradi.. Endi biz taqdimotda matematik qat'iylikka intilmaymiz. Eng muhimi, ma'noni tushunishdir.
Keling, ta'rifni eslaylik:
Hosila - bu funktsiyaning o'zgarish tezligi.
Rasmda uchta funktsiyaning grafiklari ko'rsatilgan. Sizningcha, qaysi biri tezroq o'sadi?
Javob aniq - uchinchisi. Unda eng ko'p narsa bor yuqori tezlik o'zgarishlar, ya'ni eng katta hosila.
Mana yana bir misol.
Kostya, Grisha va Matvey bir vaqtning o'zida ishga joylashdilar. Keling, ularning daromadlari yil davomida qanday o'zgarganini ko'rib chiqaylik:

Grafik bir vaqtning o'zida hamma narsani ko'rsatadi, shunday emasmi? Kostyaning daromadi olti oy ichida ikki baravar oshdi. Va Grishaning daromadi ham oshdi, lekin ozgina. Va Matveyning daromadi nolga kamaydi. Boshlanish shartlari bir xil, lekin funktsiyaning o'zgarish tezligi, ya'ni hosila, - har xil. Matveyga kelsak, uning daromadi odatda salbiy.
Intuitiv ravishda biz funktsiyaning o'zgarish tezligini osongina taxmin qilamiz. Lekin buni qanday qilamiz?
Biz haqiqatdan ham ko'rib chiqayotgan narsa bu funktsiya grafigining qanchalik keskin ko'tarilishi (yoki pastga). Boshqacha qilib aytganda, x o'zgarganda y qanchalik tez o'zgaradi? Shubhasiz, turli nuqtalarda bir xil funktsiya turli hosilaviy qiymatlarga ega bo'lishi mumkin - ya'ni u tezroq yoki sekinroq o'zgarishi mumkin.
Funktsiyaning hosilasi belgilanadi.
Grafik yordamida uni qanday topish mumkinligini sizga ko'rsatamiz.

Ayrim funksiyaning grafigi chizilgan. Keling, abtsissasi bor nuqtani olaylik. Shu nuqtada funksiya grafigiga tangens chizamiz. Biz funktsiya grafigi qanchalik keskin ko'tarilishini taxmin qilmoqchimiz. Buning uchun qulay qiymat tangens burchakning tangensi.
Funktsiyaning nuqtadagi hosilasi shu nuqtada funksiya grafigiga chizilgan tangens burchakning tangensiga teng.
E'tibor bering, tangensning moyillik burchagi sifatida biz tangens va o'qning musbat yo'nalishi orasidagi burchakni olamiz.
Ba'zan o'quvchilar funktsiya grafigiga teginish nima ekanligini so'rashadi. Bu faqat bitta bo'lgan to'g'ri chiziq umumiy nuqta grafik bilan va bizning rasmimizda ko'rsatilganidek. Bu aylanaga teguvchiga o'xshaydi.
Keling, topamiz. To'g'ri burchakli uchburchakdagi o'tkir burchakning tangensi qarama-qarshi tomonning qo'shni tomonga nisbatiga teng ekanligini eslaymiz. Uchburchakdan:
Biz funktsiya formulasini bilmagan holda grafik yordamida hosila topdik. Bunday muammolar ko'pincha matematika bo'yicha yagona davlat imtihonida raqam ostida topiladi.
Yana bir muhim munosabatlar mavjud. Eslatib o'tamiz, to'g'ri chiziq tenglama bilan berilgan
Ushbu tenglamadagi miqdor deyiladi to'g'ri chiziqning qiyaligi. U to'g'ri chiziqning o'qga moyillik burchagi tangensiga teng.
.
Biz buni tushunamiz
Keling, ushbu formulani eslaylik. Bu hosilaning geometrik ma'nosini ifodalaydi.
Funktsiyaning nuqtadagi hosilasi shu nuqtadagi funksiya grafigiga chizilgan tangensning qiyaligiga teng.
Boshqacha qilib aytganda, hosila tangens burchakning tangensiga teng.
Biz allaqachon bir xil funktsiyaning turli nuqtalarda turli hosilalarga ega bo'lishi mumkinligini aytdik. Keling, hosilaning funktsiya harakati bilan qanday bog'liqligini ko'rib chiqaylik.
Keling, qandaydir funksiyaning grafigini chizamiz. Bu funktsiya ba'zi sohalarda ko'paysin, boshqalarida kamaysin va bilan turli tezliklarda. Va bu funktsiya maksimal va minimal nuqtalarga ega bo'lsin.

Bir nuqtada funktsiya kuchayadi. Nuqtada chizilgan grafikga teginish o'tkir burchak hosil qiladi; musbat o'q yo'nalishi bilan. Bu nuqtadagi hosila ijobiy ekanligini anglatadi.
Shu nuqtada bizning funktsiyamiz pasayadi. Bu nuqtadagi tangens o'tmas burchak hosil qiladi; musbat o'q yo'nalishi bilan. O'tkir burchakning tangensi manfiy bo'lgani uchun nuqtadagi hosila manfiy bo'ladi.
Mana nima sodir bo'ladi:
Agar funktsiya ortib borayotgan bo'lsa, uning hosilasi ijobiy bo'ladi.
Agar u pasaysa, uning hosilasi salbiy hisoblanadi.
Maksimal va minimal nuqtalarda nima bo'ladi? Biz nuqtalarda (maksimal nuqta) va (minimal nuqta) tangens gorizontal ekanligini ko'ramiz. Shuning uchun, bu nuqtalarda tangens burchakning tangensi nolga teng, va hosila ham nolga teng.
Nuqta - maksimal nuqta. Bu vaqtda funksiyaning ortishi kamayish bilan almashtiriladi. Binobarin, lotin belgisi nuqtada "ortiqcha" dan "minus" ga o'zgaradi.
Nuqtada - minimal nuqta - hosila ham nolga teng, ammo uning belgisi "minus" dan "ortiqcha" ga o'zgaradi.
Xulosa: lotin yordamida biz funktsiyaning harakati haqida bizni qiziqtirgan hamma narsani bilib olamiz.
Agar hosila ijobiy bo'lsa, u holda funktsiya ortadi.
Agar hosila manfiy bo'lsa, u holda funktsiya kamayadi.
Maksimal nuqtada lotin nolga teng va belgini "ortiqcha" dan "minus" ga o'zgartiradi.
Minimal nuqtada lotin ham nolga teng va belgini "minus" dan "ortiqcha" ga o'zgartiradi.
Keling, ushbu xulosalarni jadval shaklida yozamiz:
| ortadi | maksimal nuqta | kamayadi | minimal nuqta | ortadi | |
| + | 0 | - | 0 | + |
Keling, ikkita kichik aniqlik kiritaylik. Muammoni hal qilishda sizga ulardan biri kerak bo'ladi. Boshqasi - birinchi yilda, funktsiyalar va lotinlarni jiddiyroq o'rganish bilan.
Funktsiyaning qaysidir nuqtada hosilasi nolga teng bo'lishi mumkin, lekin bu nuqtada funktsiyaning na maksimal, na minimal qiymati mavjud. Bu deb ataladigan narsa :

Bir nuqtada grafikning tangensi gorizontal, hosilasi esa nolga teng. Biroq, nuqtadan oldin funktsiya ortdi va nuqtadan keyin u o'sishda davom etmoqda. Hosilning belgisi o'zgarmaydi - u avvalgidek ijobiy bo'lib qoladi.
Bundan tashqari, maksimal yoki minimal nuqtada hosila mavjud emas. Grafikda bu ma'lum bir nuqtada tangensni chizish mumkin bo'lmaganda keskin tanaffusga to'g'ri keladi.

Funktsiya grafik bilan emas, balki formula bilan berilgan bo'lsa, hosila qanday topiladi? Bunday holda, u amal qiladi
Funktsiyani hosilasi yordamida o'rganish. Ushbu maqolada biz funktsiya grafigini o'rganish bilan bog'liq ba'zi vazifalarni tahlil qilamiz. Bunday masalalarda y = f (x) funksiyaning grafigi berilgan va funksiyaning hosilasi musbat (yoki manfiy) bo’lgan nuqtalar sonini aniqlashga oid savollar qo’yiladi. Ular funktsiyalarni o'rganish uchun hosilalarni qo'llash bo'yicha vazifalar sifatida tasniflanadi.
Bunday masalalarni va umuman tadqiqotga oid masalalarni yechish funksiyalar va hosila grafiklarini o‘rganish uchun hosila xossalarini to‘liq anglagan holdagina mumkin. Shuning uchun men sizga tegishli nazariyani o'rganishingizni qat'iy tavsiya qilaman. Siz o'rganishingiz va tomosha qilishingiz mumkin (lekin u qisqacha xulosani o'z ichiga oladi).
Kelgusi maqolalarda hosilaviy grafik berilgan muammolarni ham ko'rib chiqamiz, uni o'tkazib yubormang! Shunday qilib, vazifalar:
Rasmda (-6; 8) oraliqda aniqlangan y = f (x) funksiyaning grafigi ko'rsatilgan. Belgilang:
1. Funktsiyaning hosilasi manfiy bo'lgan butun nuqtalar soni;
2. Funksiya grafigining tangensi to'g'ri chiziqqa parallel bo'lgan nuqtalar soni y = 2;

1. Funksiyaning hosilasi funksiya kamayadigan oraliqlarda, ya’ni (−6; –3), (0; 4,2), (6,9; 8) oraliqlarda manfiy bo‘ladi. Ularda −5, −4, 1, 2, 3, 4 va 7 butun son nuqtalari mavjud. Biz 7 ball olamiz.
2. To'g'ridan-to'g'ri y= 2 o'qga parallelOhy= 2 faqat ekstremal nuqtalarda (grafik o'z xatti-harakatlarini oshirishdan kamayishgacha yoki aksincha o'zgartiradigan nuqtalarda). Bunday to'rtta nuqta mavjud: -3; 0; 4.2; 6.9
O'zingiz uchun qaror qiling:
Funktsiyaning hosilasi musbat bo'lgan butun nuqtalar sonini aniqlang.
Rasmda (-5; 5) oraliqda aniqlangan y = f (x) funksiyaning grafigi ko'rsatilgan. Belgilang:
2. Funksiya grafigining tangensi to'g'ri chiziqqa parallel bo'lgan butun nuqtalar soni y = 3;
3. Hosil nolga teng bo'lgan nuqtalar soni;

1. Funktsiya hosilasining xossalaridan ma'lumki, u funktsiya ortib boruvchi oraliqlarda, ya'ni (1,4; 2,5) va (4,4; 5) oraliqlarda musbat bo'ladi. Ularda faqat bitta butun nuqta x = 2 mavjud.
2. To'g'ridan-to'g'ri y= 3 o'qga parallelOh. Tangens chiziqqa parallel bo'ladiy= 3 faqat ekstremal nuqtalarda (grafik o'z xatti-harakatini oshirishdan pasayishga yoki aksincha o'zgartiradigan nuqtalarda).
Bunday to'rtta nuqta mavjud: -4,3; 1.4; 2,5; 4.4
3. lotin to'rt nuqtada (ekstremum nuqtalarda) nolga teng, biz ularni allaqachon ko'rsatdik.
O'zingiz qaror qiling:
f(x) funksiyaning hosilasi manfiy bo'lgan butun nuqtalar sonini aniqlang.
Rasmda (−2; 12) oraliqda aniqlangan y = f (x) funksiyaning grafigi ko'rsatilgan. Toping:
1. Funktsiyaning hosilasi musbat bo'lgan butun nuqtalar soni;
2. Funktsiyaning hosilasi manfiy bo'lgan butun nuqtalar soni;
3. Funksiya grafigining tangensi to'g'ri chiziqqa parallel bo'lgan butun nuqtalar soni y = 2;
4. Hosil nolga teng nuqtalar soni.

1. Funksiya hosilasining xossalaridan ma’lumki, u funktsiya ortib boruvchi intervallarda, ya’ni (–2; 1), (2; 4), (7; 9) va () oraliqlarda musbat bo‘ladi. 10; 11). Ularda butun nuqtalar mavjud: –1, 0, 3, 8. Ulardan jami to'rttasi bor.
2. Funksiyaning hosilasi funktsiya kamayadigan oraliqlarda, ya’ni (1; 2), (4; 7), (9; 10), (11; 12) oraliqlarda manfiy bo‘ladi. Ularda 5 va 6 sonli nuqtalar mavjud. Biz 2 ball olamiz.
3. To'g'ridan-to'g'ri y= 2 o'qga parallelOh. Tangens chiziqqa parallel bo'ladiy= 2 faqat ekstremal nuqtalarda (grafik o'z xatti-harakatlarini oshirishdan kamayishgacha yoki aksincha o'zgartiradigan nuqtalarda). Bunday nuqtalar yettita: 1; 2; 4; 7; 9; 10; 11.
4. Losin yetti nuqtada (ekstremum nuqtalarda) nolga teng, biz ularni allaqachon ko'rsatdik.
Funksiyaning uzluksizligi va differentsialligi.
Darbu teoremasi . Monotoniyaning intervallari.
Kritik nuqtalar . Ekstremum (minimal, maksimal).
Funktsiyani o'rganish dizayni.
Funktsiyaning uzluksizligi va differentsialligi o'rtasidagi bog'liqlik. Agar funktsiya f(x)bir nuqtada differentsial bo'ladi, keyin esa o'sha nuqtada uzluksiz bo'ladi. Buning aksi to'g'ri emas: uzluksiz funksiya hosilasi bo'lmasligi mumkin.
Tasvir. Agar funktsiya bir nuqtada uzilib qolsa, unda bu nuqtada uning hosilasi yo'q.

Funktsiyaning monotonligining etarli belgilari.
Agar f’(x) > 0 intervalning har bir nuqtasida (a, b), keyin f funksiyasi (x)bu oraliqda ortadi.
Agar f’(x) < 0 intervalning har bir nuqtasida (a, b) , keyin f funksiyasi(x)kamayadi bu oraliqda.
Darbu teoremasi. Funktsiyaning hosilasi 0 ga teng bo'lgan nuqtalaryoki mavjud bo'lmasa, ular funktsiyani aniqlash sohasini hosila o'z belgisini saqlab qoladigan intervallarga ajratadilar.
Ushbu intervallardan foydalanib, biz topishimiz mumkin monotonlik intervallari funktsiyalari, bu ularni o'rganishda juda muhimdir.



Shunday qilib, funktsiya intervalgacha ortadi (- , 0) va (1, + ) va intervalda kamayadi ( 0, 1). Nuqta x= 0 funktsiyaning ta'rif sohasiga kiritilmagan, lekin biz yaqinlashgandax k0 muddat x - 2 cheksiz ortadi, shuning uchun funksiya ham cheksiz ortadi. Shu nuqtadax= 1 funktsiyaning qiymati 3. Ushbu tahlilga ko'ra biz joylashtirishimiz mumkinfunktsiyaning grafigini ( 4-rasm b ) .
Kritik nuqtalar. Funktsiya sohasining ichki nuqtalari, qaysi ichida hosilasi ga teng null yoki mavjud emas, chaqiriladi tanqidiy nuqta bu funksiya. Funktsiyani tahlil qilish va uning grafigini tuzishda bu nuqtalar juda muhim, chunki faqat shu nuqtalarda funktsiyaga ega bo'lishi mumkin. ekstremum (minimal yoki maksimal , 5-rasm A,b).

Nuqtalarda x 1 , x 2 (5-rasm a) Va x 3 (5-rasm b) hosilasi 0; nuqtalarda x 1 , x 2 (5-rasm b) hosila mavjud emas. Ammo ularning barchasi ekstremal nuqtalardir.
Ekstremum uchun zaruriy shart. Agar x 0 - funksiyaning ekstremum nuqtasi f(x) va f' hosilasi shu nuqtada mavjud bo'lsa, f'(x 0)= 0.
Bu teorema zarur ekstremal holat. Agar biror nuqtada funktsiyaning hosilasi 0 bo'lsa, bu degani emas funktsiya bu nuqtada ekstremumga ega. Masalan, funktsiyaning hosilasif (x) = x 3 da 0 ga teng x= 0, lekin bu funktsiyada bu nuqtada ekstremum yo'q (6-rasm).

Boshqa tomondan, funktsiyay = | x| , 3-rasmda keltirilgan, nuqtada minimumga egax= 0, lekin bu nuqtada hosila mavjud emas.
Ekstremum uchun etarli sharoitlar.
X nuqtadan o'tayotganda hosila bo'lsa 0 uning belgisini ortiqcha dan minusga o'zgartiradi, keyin x 0 - maksimal nuqta.
X nuqtadan o'tayotganda hosila bo'lsa 0 uning belgisini minusdan ortiqcha ga o'zgartiradi, keyin x 0 - minimal ball.
Funktsiyani o'rganish dizayni. Funktsiya grafigini chizish uchun sizga kerak bo'ladi:
1) funktsiyaning ta'rif sohasi va qiymatlari oralig'ini toping;
2) funksiyaning juft yoki toq ekanligini aniqlash;
3) funksiya davriy yoki davriy emasligini aniqlash;
4) funksiyaning nollarini va uning qiymatlarini topingx = 0,
5) doimiy ishorali intervallarni toping;
6) monotonlik oraliqlarini toping;
7) ekstremum nuqtalarni va ushbu nuqtalarda funktsiya qiymatlarini toping;
8) funksiyaning “yakka” nuqtalar yaqinidagi harakatini tahlil qiling
Va qachon katta qiymatlar modulx .
MISOL Funktsiyani o'rganingf(x) = x 3 + 2 x 2 - x- 2 va grafik chizing.
Yechish funksiyani yuqoridagi sxema bo‘yicha o‘rganamiz.
1) ta'rif sohasixR (x- har qanday haqiqiy raqam);
Qiymatlar diapazoniyR , chunki f (x) – toq ko‘phad
darajalar;
2) funktsiya f (x) juft ham, toq ham emas
(iltimos tushuntiring);
3) f (x) davriy bo‘lmagan funksiya (o‘zingiz isbotlang);
4) funksiya grafigi o‘qni kesib o‘tadiY nuqtada (0, - 2),
Chunki f (0) = - 2 ; kerakli funksiyaning nollarini topish uchun
Tenglamani yeching:x 3 + 2 x 2 - x - 2 = 0, ildizlardan biri
qaysi ( x= 1) aniq. Boshqa ildizlar
(agar ular mavjud bo'lsa! ) kvadrat tenglamani yechishdan:
x 2 + 3 x+ 2 = 0, bu ko'phadni bo'lish orqali olinadi
x 3 + 2 x 2 - x- har binom uchun 2 ( x– 1). Tekshirish oson
Qolgan ikkita ildiz nima:x 2 = - 2 va x 3 = - 1. Shunday qilib,
Funktsiyaning nollari: - 2, - 1 va 1.
5) Demak, son o'qi bu ildizlarga bo'linadi
Belgining doimiyligining to'rtta oralig'i, ular ichida
Funktsiya o'z belgisini saqlab qoladi:
Ushbu natijani kengaytirish orqali olish mumkin
polinom omillarga:
x 3 + 2 x 2 - x - 2 = (x + 2) (x + 1 (x – 1)
Va ishning belgisini baholash .
6) hosila f' (x) = 3 x 2 + 4 x- 1 nuqtada hech qanday nuqta yo'q
U mavjud emas, shuning uchun uning ta'rif sohasiR (Hammasi
Haqiqiy raqamlar); nollarf' (x) tenglamaning ildizlari:
3 x 2 + 4 x- 1 = 0 .

Olingan natijalar jadvalda umumlashtiriladi: