На данном уроке мы продолжим изучение степенных функций с рациональным показателем, рассмотрим функции с отрицательным рациональным показателем.
1. Основные понятия и определения
Напомним свойства и графики степенных функций с целым отрицательным показателем.
При четных n, :
Пример функции:
Все графики таких функций проходят через две фиксированные точки: (1;1), (-1;1). Особенность функций данного вида - их четность, графики симметричны относительно оси ОУ.

Рис. 1. График функции
При нечетных n, :
Пример функции:
Все графики таких функций проходят через две фиксированные точки: (1;1), (-1;-1). Особенность функций данного вида - их нечетность, графики симметричны относительно начала координат.

Рис. 2. График функции
2. Функция с отрицательным рациональным показателем степени, графики, свойства
Напомним основное определение.
Степенью неотрицательного числа а с рациональным положительным показателем называется число .
Степенью положительного числа а с рациональным отрицательным показателем называется число .
Для выполняется равенство:
![]()
![]()
Например: ![]() ; - выражение не существует по определению степени с отрицательным рациональным показателем; существует, т. к. показатель степени целый,
; - выражение не существует по определению степени с отрицательным рациональным показателем; существует, т. к. показатель степени целый,![]()
Перейдем к рассмотрению степенных функций с рациональным отрицательным показателем.
![]()
Например:
Для построения графика данной функции можно составить таблицу. Мы поступим иначе: сначала построим и изучим график знаменателя - он нам известен (рисунок 3).

Рис. 3. График функции
График функции знаменателя проходит через фиксированную точку (1;1). При построении графика исходной функции данная точка остается, при корень также стремится к нулю, функция стремится к бесконечности. И, наоборот, при стремлении х к бесконечности функция стремится к нулю (рисунок 4).

Рис. 4. График функции
Рассмотрим еще одну функцию из семейства изучаемых функций.
![]()
Важно, что по определению
Рассмотрим график функции, стоящей в знаменателе: , график данной функции нам известен, она возрастает на своей области определения и проходит через точку (1;1) (рисунок 5).

Рис. 5. График функции
При построении графика исходной функции точка (1;1) остается, при корень также стремится к нулю, функция стремится к бесконечности. И, наоборот, при стремлении х к бесконечности функция стремится к нулю (рисунок 6).

Рис. 6. График функции
Рассмотренные примеры помогают понять, каким образом проходит график и каковы свойства изучаемой функции - функции с отрицательным рациональным показателем.
Графики функций данного семейства проходят через точку (1;1), функция убывает на всей области определения.
Область определения функции: ![]()
Функция не ограничена сверху, но ограничена снизу. Функция не имеет ни наибольшего, ни наименьшего значения.
Функция непрерывна, принимает все положительные значения от нуля до плюс бесконечности.
Функция выпукла вниз (рисунок 15.7)
На кривой взяты точки А и В, через них проведен отрезок, вся кривая находится ниже отрезка, данное условие выполняется для произвольных двух точек на кривой, следовательно функция выпукла вниз. Рис. 7.

Рис. 7. Выпуклость функции
3. Решение типовых задач
Важно понять, что функции данного семейства ограничены снизу нулем, но наименьшего значения не имеют.
Пример 1 - найти максимум и минимум функции на интервале \[{\mathop{lim}_{x\to +\infty } x^{2n}\ }=+\infty \]
График (рис. 2).

Рисунок 2. График функции $f\left(x\right)=x^{2n}$
Свойства степенной функции с натуральным нечетным показателем
Область определения -- все действительные числа.
$f\left(-x\right)={(-x)}^{2n-1}={-x}^{2n}=-f(x)$ -- функция нечетна.
$f(x)$ - непрерывна на всей области определения.
Область значения -- все действительные числа.
$f"\left(x\right)=\left(x^{2n-1}\right)"=(2n-1)\cdot x^{2(n-1)}\ge 0$
Функция возрастает на всей области определения.
$f\left(x\right)0$, при $x\in (0,+\infty)$.
$f{""\left(x\right)}={\left(\left(2n-1\right)\cdot x^{2\left(n-1\right)}\right)}"=2\left(2n-1\right)(n-1)\cdot x^{2n-3}$
\ \
Функция вогнута, при $x\in (-\infty ,0)$ и выпукла, при $x\in (0,+\infty)$.
График (рис. 3).
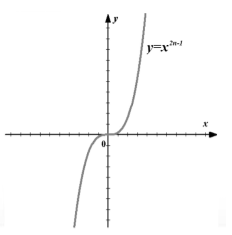
Рисунок 3. График функции $f\left(x\right)=x^{2n-1}$
Степенная функция с целым показателем
Для начала введем понятие степени с целым показателем.
Определение 3
Степень действительного числа $a$ c целым показателем $n$ определяется формулой:

Рисунок 4.
Рассмотрим теперь степенную функцию с целым показателем, её свойства и график.
Определение 4
$f\left(x\right)=x^n$ ($n\in Z)$ называется степенной функцией с целым показателем.
Если степень больше нуля, то мы приходим к случаю степенной функции с натуральным показателем. Его мы уже рассмотрели выше. При $n=0$ мы получим линейную функцию $y=1$. Её рассмотрение оставим читателю. Осталось рассмотреть свойства степенной функции с отрицательным целым показателем
Свойства степенной функции с отрицательным целым показателем
Область определения -- $\left(-\infty ,0\right)(0,+\infty)$.
Если показатель четный, то функция четна, если нечетный, то функция нечетна.
$f(x)$ - непрерывна на всей области определения.
Область значения:
Если показатель четный, то $(0,+\infty)$, если нечетный, то $\left(-\infty ,0\right)(0,+\infty)$.
При нечетном показателе функция убывает, при $x\in \left(-\infty ,0\right)(0,+\infty)$. При четном показателе функция убывает при $x\in (0,+\infty)$. и возрастает, при $x\in \left(-\infty ,0\right)$.
$f(x)\ge 0$ на всей области определения
Урок и презентация на тему: "Степенные функции. Свойства. Графики"
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине "Интеграл" для 11 класса
Интерактивное пособие для 9–11 классов "Тригонометрия"
Интерактивное пособие для 10–11 классов "Логарифмы"
Степенные функции, область определения.
Ребята, на прошлом уроке мы узнали, как работать с числами с рациональным показателем степени. На этом уроке мы рассмотрим степенные функции и ограничимся случаем, когда показатель степени рациональный.Мы будем рассматривать функции вида: $y=x^{\frac{m}{n}}$.
Рассмотрим сначала функции, у которых показатель степени $\frac{m}{n}>1$.
Пусть нам дана конкретная функция $y=x^2*5$.
Согласно определению, которое мы дали на прошлом уроке: если $x≥0$, то есть область определения нашей функции - это луч ${x}$. Давайте схематично изобразим наш график функции.

Свойства функции $y=x^{\frac{m}{n}}$, $0 2. Не является ни четной, ни нечетной.
3. Возрастает на $$,
б) $(2,10)$,
в) на луче $$.
Решение.
Ребята, вы помните как мы находили наибольшее и наименьшее значение функции на отрезке в 10 классе?
Правильно, мы использовали производную. Давайте решим наш пример и повторим алгоритм поиска наименьшего и наибольшего значения.
1. Найдем производную заданной функции:
$y"=\frac{16}{5}*\frac{5}{2}x^{\frac{3}{2}}-x^3=8x^{\frac{3}{2}}-x^3=8\sqrt{x^3}-x^3$.
2. Производная существует на всей области определения исходной функции, тогда критических точек нет. Найдем стационарные точки:
$y"=8\sqrt{x^3}-x^3=0$.
$8*\sqrt{x^3}=x^3$.
$64x^3=x^6$.
$x^6-64x^3=0$.
$x^3(x^3-64)=0$.
$x_1=0$ и $x_2=\sqrt{64}=4$.
Заданному отрезку принадлежит только одно решение $x_2=4$.
Построим таблицу значений нашей функции на концах отрезка и в точке экстремума:
Ответ: $y_{наим.}=-862,65$ при $x=9$; $y_{наиб.}=38,4$ при $x=4$.
Пример. Решить уравнение: $x^{\frac{4}{3}}=24-x$.
Решение. График функции $y=x^{\frac{4}{3}}$ возрастает, а график функции $у=24-х$ убывает. Ребята, мы с вами знаем: если одна функция возрастает, а другая убывает, то они пересекаются только в одной точке, то есть у нас только одно решение.
Заметим:
$8^{\frac{4}{3}}=\sqrt{8^4}=(\sqrt{8})^4=2^4=16$.
$24-8=16$.
То есть при $х=8$ мы получили верное равенство $16=16$, это и есть решение нашего уравнения.
Ответ: $х=8$.
Пример.
Построить график функции: $y=(x-3)^\frac{3}{4}+2$.
Решение.
График нашей функции получается из графика функции $y=x^{\frac{3}{4}}$, смещением его на 3 единицы вправо и 2 единицы вверх.

Пример. Составить уравнение касательной к прямой $y=x^{-\frac{4}{5}}$ в точке $х=1$.
Решение. Уравнение касательной определяется известной нам формулой:
$y=f(a)+f"(a)(x-a)$.
В нашем случае $a=1$.
$f(a)=f(1)=1^{-\frac{4}{5}}=1$.
Найдем производную:
$y"=-\frac{4}{5}x^{-\frac{9}{5}}$.
Вычислим:
$f"(a)=-\frac{4}{5}*1^{-\frac{9}{5}}=-\frac{4}{5}$.
Найдем уравнение касательной:
$y=1-\frac{4}{5}(x-1)=-\frac{4}{5}x+1\frac{4}{5}$.
Ответ: $y=-\frac{4}{5}x+1\frac{4}{5}$.
Задачи для самостоятельного решения
1. Найти наибольшее и наименьшее значение функции: $y=x^\frac{4}{3}$ на отрезке:а) $$.
б) $(4,50)$.
в) на луче $$.
3. Решить уравнение: $x^{\frac{1}{4}}=18-x$.
4. Построить график функции: $y=(x+1)^{\frac{3}{2}}-1$.
5. Составить уравнение касательной к прямой $y=x^{-\frac{3}{7}}$ в точке $х=1$.
Степенной называется функция вида y=x n (читается как y равно х в степени n), где n – некоторое заданное число. Частными случаями степенных функций является функции вида y=x, y=x 2 , y=x 3 , y=1/x и многие другие. Расскажем подробнее о каждой из них.
Линейная функция y=x 1 (y=x)
График прямая линия, проходящая через точку (0;0) под углом 45 градусов к положительному направлению оси Ох.
График представлен ниже.
Основные свойства линейной функции:
- Функция возрастающая и определена на всей числовой оси.
- Не имеет максимального и минимального значений.
Квадратичная функция y=x 2
Графиком квадратичной функции является парабола.

Основные свойства квадратичной функции:
- 1. При х =0, у=0, и у>0 при х0
- 2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.
- 3. Функция убывает на промежутке (-∞;0] и возрастает на промежутке }